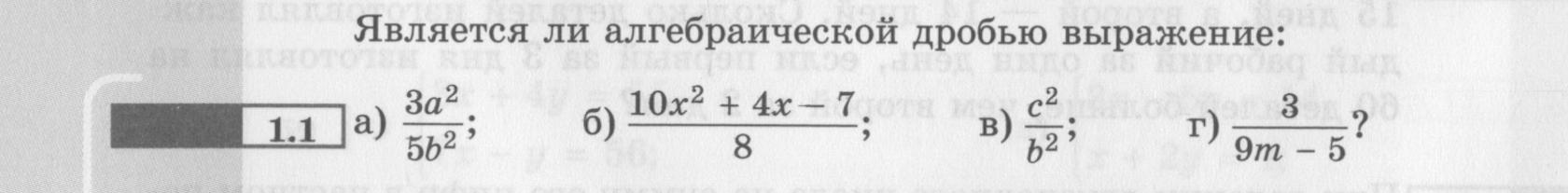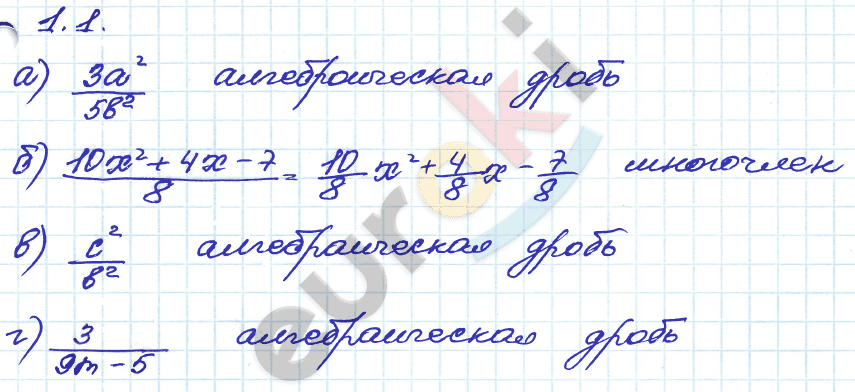ГДЗ Алгебра 8 класс Мордкович, Александрова, Мишустина - Сборник задач

- Алгебра 8 класс
- Тип пособия: Сборник задач
- Издательство: «Мнемозина»
Глава 1. Алгебраические дроби. §1. Основные понятия
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41Глава 1. Алгебраические дроби. Домашняя контрольная работа №1
Вариант 1 Вариант 2Глава 1. Алгебраические дроби. §2. Основное свойство алгебраической дроби
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48Глава 1. Алгебраические дроби. §3. Сложение и вычитание алгебраических дробей с одинаковыми знаменателями
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29Глава 1. Алгебраические дроби. §4. Сложение и вычитание алгебраических дробей с разными знаменателями
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56Глава 1. Алгебраические дроби. §5. Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46Глава 1. Алгебраические дроби. §6. Преобразование рациональных выражений
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24Глава 1. Алгебраические дроби. §7. Первые представления о рациональных уравнениях
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40Глава 1. Алгебраические дроби. §8. Степень с отрицательным целым показателем
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32Глава 2. Функция y = √x. Свойства квадратного корня. Домашняя контрольная работа №2
Вариант 1 Вариант 2Глава 2. Функция y = √x. Свойства квадратного корня. §9. Рациональные числа
1 2 3 4 5 6 7Глава 2. Функция y = √x. Свойства квадратного корня. §10. Понятие квадратного корня из неотрицательного числа
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29Глава 2. Функция y = √x. Свойства квадратного корня. §11. Иррациональные числа
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43Глава 2. Функция y = √x. Свойства квадратного корня. §12. Множество действительных чисел
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17Глава 2. Функция y = √x. Свойства квадратного корня. §13. Функция y = √x, её свойства и график
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22Глава 2. Функция y = √x. Свойства квадратного корня. §14. Свойства квадратных корней
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32Глава 2. Функция y = √x. Свойства квадратного корня. §15. Преобразование выражений, содержащих операции извлечения квадратного корня
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36Глава 2. Функция y = √x. Свойства квадратного корня. §16. Модуль действительного числа
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99Глава 3. Функция у = к:х, её свойства и график. Домашняя контрольная работа №3
Вариант 1 Вариант 2Глава 3. Функция у = к:х, её свойства и график. §17. Функция у = к(х)^2, её свойства и график
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44Глава 3. Функция у = к:х, её свойства и график. §18. Функция у = к:х, её свойства и график
1 2 3 4 5 6 7Глава 3. Функция у = к:х, её свойства и график. §19. Как построить график функции у = f(х+l), если известен график функции у = f(х)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66Глава 3. Функция у = к:х, её свойства и график. §20. Как построить график функции у = f(х) + m, если известен график функции у = f(х)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38Глава 3. Функция у = к:х, её свойства и график. §21. Как построить график функции у = f(х + l) + m, если известен график функции у = f(х)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58Глава 3. Функция у = к:х, её свойства и график. §22. Функция y = ax^2 + bx + c, её свойства и график
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42Глава 4. Квадратные уравнения. Домашняя контрольная работа №4
Вариант1 Вариант2Глава 4. Квадратные уравнения. §23. Графическое решение квадратных уравнений
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29Глава 4. Квадратные уравнения. §24. Основные понятия
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55Глава 4. Квадратные уравнения. §25. Формулы корней квадратных уравнений
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24Глава 4. Квадратные уравнения. §26. Рациональные уравнения
1 2 3 4 5 6 7Глава 4. Квадратные уравнения. §27. Рациональные уравнения, как математические модели реальных ситуаций
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39Глава 4. Квадратные уравнения. §28. Ещё одна формула корней квадратного уравнения
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48Глава 4. Квадратные уравнения. §29. Теорема Виета
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28Глава 4. Квадратные уравнения. §30. Иррациональные уравнения
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45Глава 5. Неравенства. Домашняя контрольная работа №5
Вариант1 Вариант2Глава 5. Неравенства. §31. Свойства числовых неравенств
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28Глава 5. Неравенства. §32. Исследование функций на монотонность
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55Глава 5. Неравенства. §33. Решение линейных неравенств
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24Глава 5. Неравенства. §34. Решение квадратных неравенств
1 2 3 4 5 6 7Глава 5. Неравенства. §35. Приближенные значения действительных чисел
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65Глава 5. Неравенства. §36. Стандартный вид числа
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37Глава 6. §37
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46Глава 6. §38
1 2 3 4 5 6 7 8 9 10 11Глава 6. §39
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19Глава 6. §40
1 2 3 4 5 6 7Глава 6. Итоговое повторение
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158Задачи на повторение
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68Похожие ГДЗ Алгебра 8 класс

- Алгебра 7-9 класс
- Тетрадь для контрольных работ
- Мордкович
- Мнемозина

- Алгебра 8 класс
- Тесты
- Мордкович, Турчинская
- Вентана-Граф

- Алгебра 8 класс
- Рабочая тетрадь
- УМК
- Ключникова, Комиссарова
- Экзамен
- 1,2

- Алгебра 7-9 класс
- Тесты
- Мордкович, Тульчинская
- Мнемозина
Алгебра не бывает легкой
Порой кажется, что алгебра относится к тем предметам, которые просто невозможно понять. Но не стоит так отчаиваться. Не бывает недостижимых целей, иногда просто приложено недостаточно усилий. Поэтому даже эти уроки можно полюбить, если в достаточной степени разобраться с алгоритмом решения уравнений и с основными понятиями формул. Помимо этого требуется непрестанная практика в работе с примерами. Поэтому непременными условиями успешного обучения являются:
- Внимательность.
- Трудолюбие.
- Усердие.
К данному предмету стоит подходить очень серьезно, если ребята стремятся добиться по-настоящему отличных результатов. Но довольно часто на пути к хорошим оценкам возникают довольно серьезные препятствия. И чаще всего они связаны с элементарным недопониманием тематики. А этого допускать нельзя, ведь очень скоро школьникам придется доказывать свои знания во время экзаменов. Помочь ученику разобраться со сложной для него наукой поможет решебник «Алгебра 8 класс Сборник задач Мордкович».
Что можно найти в ГДЗ
Пособие разделено на шесть глав, причем в последней из них даются итоговые задания для повторения материала. «ГДЗ по Алгебре 8 класс Мордкович (Мнемозина)» имеет подробные примеры решений для всех задач из школьного курса. Авторы предусмотрительно внесли по несколько путей нахождения ответа, которые содержат различные алгоритмы, чтобы ученики сами определились с нужным.
Что дает использование решебника
Первое, что необходимо сделать учащимся, если они хотят получить полноценные знания, а не разрозненную информацию — это вникнуть в суть изучаемого материала. Только это поможет разобраться в алгоритме решений, а также применять его в дальнейшем на практике. Но вместо того, чтобы справляться с возникающими затруднениями, многие подростки предпочитают:
- отложить все на потом;
- списать д/з;
- заняться чем-нибудь более интересным.
При таком подходе совсем не удивительно, что в дневниках не сияют пятерки, а учителя все время ругают и норовят сделать замечание. Поэтому ребятам очень пригодиться ГДЗ, при помощи которых они могут ознакомиться с разнообразием способов решений примеров. Решебник «Алгебра 8 класс Мордкович (Мнемозина)» поможет подготовиться к самостоятельным работам, научит не бояться отвечать у доски и даст чувство уверенности.
Стоит ли применять решебники в учебе
Восьмиклассникам в наше время приходится весьма непросто, ведь на них постоянно давят со всех сторон. И родители, и учителя в унисон твердят о предстоящих в следующем году экзаменах, об ответственности, о том, как важно тщательно все учить. Но у ребят порой не хватает времени на то, чтобы полноценно выполнить все задаваемые на день д/з. Помимо этого приходится посещать дополнительные обязательные факультативы, кроме того, многие подростки посещают какие-то секции и кружки. Не сидеть же над уроками до поздней ночи? А ведь делать что-то нужно, ведь успеваемость по многим предметам, в том числе и по алгебре начинает стремительно падать.
Многое в это время зависит от преподавателей - насколько грамотно они смогут подать учебный материал. Но, к сожалению, в большинстве случаев школьникам предстоит самостоятельно разбирать каждую тему. Естественно, при этом может возникнуть много недопониманий. Спросить же разъяснений ребятам зачастую не у кого. Вот и получается, что вместо знаний они приобретают одни вопросы. Однако не стоит отчаиваться, есть вполне реальный способ преодолеть все недопонимания и проработать слабые моменты.
Некоторые взрослые упорно придерживаются версии, что исправить все ошибки учащихся способен только репетитор. Но это далеко не так, ведь при таком подходе ребята постоянно ждут подсказки и порой ленятся до такой степени, что это лишь ухудшает их результаты на уроках. Как же помочь подросткам лучше разобраться в материале? Ответ очень прост - использовать сборники ГДЗ. Конечно, не обойдется и без случаев списывания, но очень скоро ученики убедятся, что такой подход не принесет им ощутимой пользы и начнут использовать пособия по назначению.
Как именно нужно использовать ГДЗ
Родители зачастую не верят в пользу решебников, считая это очередной прихотью и блажью ленивых ребят. Для них ГДЗ - это просто шпаргалка. Но даже специалисты в области образования сейчас признают, что именно эти пособия позволяют многим ученикам полноценно разобрать все премудрости учебного материала на наглядных примерах. Так что не стоит запрещать школьникам пользоваться сборниками, нужно просто объяснить, как делать это правильно:
- Не стоит игнорировать изучение теории.
- Все задания необходимо выполнять самостоятельно.
- При проверке ответов нужно использовать ГДЗ.
- Всегда следует внимательно изучать обнаруженные ошибки.
- Если требуется, надо закрепить материал.
Алгебра совсем непростой предмет, поэтому к ее изучению стоит подходить предельно внимательно. Но есть ребята, которые просто не понимают эту дисциплину, так как имеют гуманитарный склад ума. Это, конечно же, не избавляет их от необходимости писать контрольные, тесты или экзамены. Поэтому иметь твердые знания алгебраических законов должны все школьники. Использование ГДЗ по алгебре 8 класс Сборник задач Мордкович (Мнемозина) поможет им в этом.
Если подходить к работе с решебником правильно, то можно:
- тщательно вникнуть в суть теоретического материала;
- запомнить все необходимые алгоритмы;
- проработать имеющиеся слабые моменты;
- повторить информацию перед предстоящей проверкой знаний, и т.д.
Замечено, что систематическое применение ГДЗ приводит не только к улучшению оценок по предмету, но и к стабилизации психологического состояния учащихся. Они перестают нервничать из-за предстоящих уроков или переживать, что что-то не успеют. С представленным пособием время на выполнение д/з существенно сокращается, что позволит ребятам больше уделять его своим личным делам или отдыху. Кроме того, их родители увидят, что дети самостоятельно преодолевают трудности и перестанут постоянно давить на них.